ALGUNOS TIPOS DE MATRICES

• ALGUNOS TIPOS DE MATRICES

Hay algunas matrices que aparecen frecuentemente y que según su forma, sus elementos, ... reciben nombres diferentes :

Tipo de matriz	Definición	Ejemplo
FILA	Aquella matriz que tiene una sola fila, siendo su orden  1×n
COLUMNA	Aquella matriz que tiene una sola columna, siendo su orden  m×1
RECTANGULAR	Aquella matriz que tiene distinto número de filas que de columnas, siendo su orden  m×n ,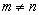
TRASPUESTA	Dada una matriz  A, se llama traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas. Se representa por  At  ó  AT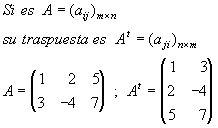
OPUESTA	La matriz opuesta de una dada es la que resulta de sustituir cada elemento por su opuesto. La opuesta de  A  es   -A.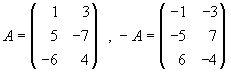
NULA	Si todos sus elementos son cero. También se denomina matriz cero y se denota por 0m×n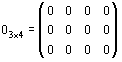
CUADRADA	Aquella matriz que tiene igual número de filas que de columnas, m = n, diciendose que la matriz es de orden n. Diagonal principal : son los elementos  a11 , a22 , ..., ann Diagonal secundaria : son los elementos  aij con   i+j = n+1 Traza de una matriz cuadrada : es la suma de los elementos de la diagonal principal tr A.	Diagonal principal : Diagonal secundaria :
SIMÉTRICA	Es una matriz cuadrada que es igual a su traspuesta. A = At  , aij = aji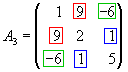
ANTISIMÉTRICA	Es una matriz cuadrada que es igual a la opuesta de su traspuesta. A = -At  , aij = -aji Necesariamente  aii = 0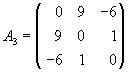
DIAGONAL	Es una matriz cuadrada que tiene todos sus elementos nulos excepto los de la diagonal principal
ESCALAR	Es una matriz cuadrada que tiene todos sus elementos nulos excepto los de la diagonal principal que son iguales
IDENTIDAD	Es una matriz cuadrada que tiene todos sus elementos nulos excepto los de la diagonal principal que son iguales a 1.Tambien se denomina matriz unidad.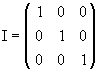
TRIANGULAR	Es una matriz cuadrada que tiene todos los elementos por encima (por debajo) de la diagonal principal nulos.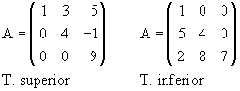
ORTOGONAL	Una matriz ortogonal es necesariamente cuadrada e invertible :  A-1 = AT La inversa de una matriz ortogonal es una matriz ortogonal. El producto de dos matrices ortogonales es una matriz ortogonal. El determinante de una matriz ortogonal vale +1 ó -1.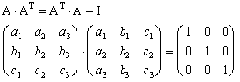
NORMAL	Una matriz es normal si conmuta con su traspuesta. Las matrices simétricas, antisimétricas u ortogonales son necesariamente normales.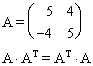
INVERSA	Decimos que una matriz cuadrada  A   tiene inversa, A-1, si se verifica que : A·A-1 = A-1·A = I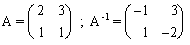

Para establecer las reglas que rigen el cálculo con matrices se desarrolla un álgebra semejante al álgebra ordinaria, pero en lugar de operar con números lo hacemos con matrices.